At Kingsbury Academy, we have embarked on a research journey focusing on our "My Thinking and Problem-solving" curriculum. This curriculum is designed to help learners embed essential mathematical skills. Additionally, our My Maths curriculum aims to bridge gaps to the national curriculum while ensuring that learners can generalise their knowledge across various contexts, demonstrating the coherence of our curriculum sequencing.

Our research will delve into rich qualitative learning experiences across the school, exploring how the NCTEM "Teaching for Mastery" principles can be applied in a special education setting. We will present our findings at the Mathematical Association's "Access for All" conference this September 2024 and in a podcast hosted by Alan Edmiston, a renowned maths specialist. Alan is an editor of the Maths Associations SEND publication Equals online and has a real passion for helping teachers understand cognitive development and how to apply this to enhance learning in all classrooms. Alan is further recognised for being a Partnership Advisor for STEM learning and working with special schools developing science provision as well as leading them nationally.  

How representations have been used to scaffold mathematical enquiry.

Visual supports here are used to support learners in ‘seeing maths’ so they can build on connections and have a deeper understanding of concepts including.

 

 

 

  

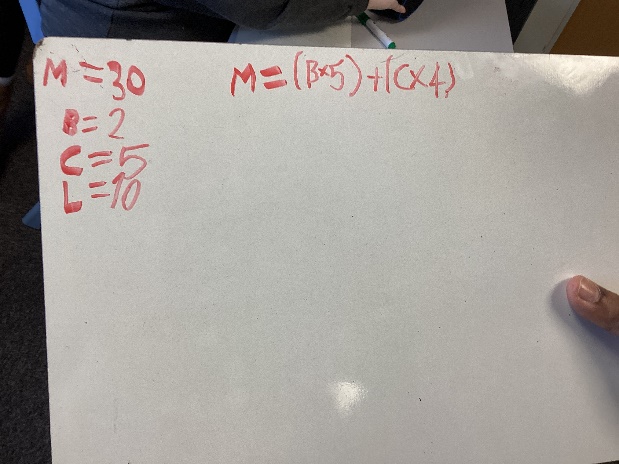
Mathematical Thinking

Mathematical thinking is central to how pupils learn mathematics and includes looking for patterns and relationships, making connections, conjecturing, reasoning, and generalising. Learners should actively engage in mathematical thinking in all lessons, having opportunities to practice, maintain and extend learning. 

  

Fluency

Efficient, accurate recall of key numbers, facts and procedures is essential for fluency, freeing pupils’ minds to think deeply about concepts and problems, but fluency demands more than this. It requires pupils to have the flexibility to move between different contexts and representations of mathematics, to recognise relationships and make connections, and to choose appropriate methods and strategies to solve problems. In this sense, we look at the way in which key skills, including visual, modelling, problem-solving and number come together as the foundations for fluency. This approach to developing secure attention, matching, imitation, spatial awareness and sorting are instrumental to the pedagogical underpinnings of mathematics. Have a look at our interactive staff CPD sessions below:

    

Variation

The purpose of variation is to draw closer attention to a key feature of a mathematical concept or structure through varying some elements while keeping others constant.

• Conceptual variation involves varying how a concept is represented to draw attention to critical features. Often, more than one representation is required to look at the concept from different perspectives and gain comprehensive knowledge.